⑥ オッズ比*1
少し脱線したので本線に戻して、EBMの解説を続ける。オッズという言葉があるが、通常使われるのは競馬の払い戻し率などの賭け事や戦いにおける勝算や賭け率である。オッズ比は言うなれば、当たる確率と外れる確率の比のことである。当たる確率がpならば、外れる確率は1‐pなのでオッズ比はp/(1‐p)で表され、pの逆数1/pでないことに注意する。オッズ比が1ということは、当たる確率と外れる確率が同じことを意味しており、当たる確率が60%ならばオッズ比は1.5となり、確率が40%ならばオッズ比は0.67となって、確率の差異(1.5倍)以上に大きな差(2.25倍)として表現される。
癌検診の有効性を示す指標としてオッズ比が用いられる。実は癌検診の場合には日本ではRCTが行われていないのが現状である。慶応大学の近藤誠講師の言い分も正に其処にある。海外でもあまり行われておらず、その中では大腸癌を対象にして3つのRCTがあり、便潜血反応による大腸癌の検診の有効性を既に証明されているとの事であるが、肺癌を対象に行われた3つのRCTではすべて否定的な結果になっているとの事で、それ以外はあまりないようである。その他の乳癌、子宮頚癌、胃癌の検診では世界でも行われてないのが現状である1)。
ここには当然倫理の問題が絡んできており、「集団検診が既に有効であることがわかっている癌に対してRCTを実施するのは、人為的に検診を受けない人を作ってしまうことになり倫理上許されない」(自治医大斎藤教授)という考え方からである。
ところが、肺癌のオッズ比は0.72(有効とは言えない数値)で胃癌は 0.4程度(有効といえる値)というような数値が言われているし、斎藤教授の言にあるように既に有効であるということがわかっているという。それはどうして「わかった」のかというと、RCTでなく症例対象研究(その5参照:平成12年8月号)で「わかった」ということである。
すなわち、ある癌で死亡した症例群と、背景が同一な対照群を設定し、両群の検診歴を調べる。そしてそれらを併せて、検診を受けた人がその癌で死ぬリスクのオッズ比を表すのである。
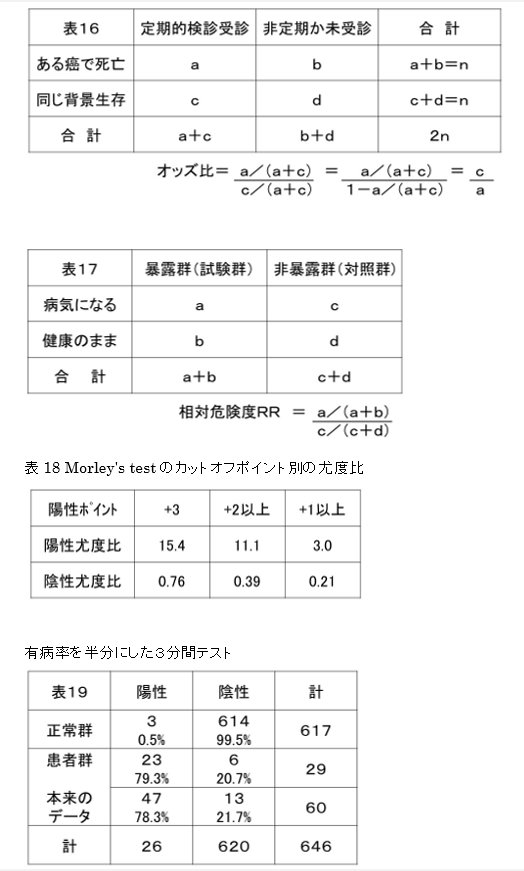
例えば、表16である癌で死んだ人と同等の背景(性別・年齢・既往歴・病態・入院か否かなどでなるべく同じになるように)を持った同数の生存者を選択する。この人数をn人ずつとすると合計は2nとなる。この中から、癌で死亡したが検診を定期的に受診している人をa人、癌で死亡して受診してない人をb人、対照の生存者で検診を受けている人をc人、受けてない人をd人とする。そうすると2n人の中で定期的に検診を受けた人は(a+c)人で、非受診者は(b+d)人となる。検診を受けていた人で死亡者の割合(死ぬリスク)はa/(a+c)であり、検診を受けていた人で生存者の割合は1-a/(a+c)=c/(a+c)でこの二つの割合の比がオッズ比である。そして死亡者の割合を分子に、生存者の割合を分母にとれば、オッズ比が小さいほど検診の有効性をいうことができる。
こういうケースは、後ろ向きの症例対照研究であり、対照は決して同一の背景ということは実際にはあり得ないというような様々な問題が当然あってエビデンスの質は低いが、幾つもの症例対照研究が同じように有効であることを示していればそれは有効といえるでしょう、というのが今の日本の医学会のコンセサンス(共通認識)である。しかし、日本では既に検診が行われるようになってから、これらの症例対照研究が行われてきたケースがほとんどであり、まず検診有りきという立場になっていて、検診に否定的な見解は出にくい状況になっている。
胃癌の検診は海外では発症率が少ないということがあって日本だけで実施されているようであり、その症例対照研究によるオッズ比は概ね0.4程度(検診を行っている人の方が死亡率が4割程度であるということではないことに注意)あり、検診の実施により死亡率が減少しているので検診の有効性がいわれているが、検診を行ってない海外でも胃癌の死亡率は減少してきているという実態が有る。これは冷蔵庫などの普及により相対的に塩分の摂取量が減っているためと説明されている(最近ではヘリコバクター・ピロリ菌との関連もいわれているが)。そうなると、日本での死亡率低下も検診のためなのか、冷蔵庫や塩分を控えることが普及してきたためか分からなくなってくる。
このようなことや検診による放射線被爆等の種々の肉体的損失などを考えると近藤講師の「癌検診を拒否せよ」という言葉は、全く荒唐無稽とはいい難いのである。実際にこのような二次予防(早期発見)よりも一次予防(病気にならないようにする:いわゆる未病治)の方が重要であるという見解が徐々に浸透し始めているようにもなってきている。米国では、嫌煙・禁煙運動の結果肺癌のみならず、癌全体の有病率が減少しているとのことである。
⑦ 相対危険度*2
オッズ比に似たような概念を表す言葉に、相対危険度がある。これは暴露群(EX.治療群や検診を行った群など)が病気になるリスク(危険)を非暴露群(EX.何もしない群)が病気になるリスクで割ったものをいう。
表17では、暴露群のリスクは、a/(a+b)で、非暴露群のリスクはc/(c+d)であるから、相対危険度(RR)={a/(a+b)}/{c/(c+d)}となる。
コホート研究で、例えばインフルエンザワクチン接種した群や煙草を止めた群(暴露群)がインフルエンザになったり、肺癌になったりする確率をワクチンを接種してないでインフルエンザになったり、煙草を吸っていて肺癌になった確率で割ったものをいう。
すなわち、前者ではインフルエンザワクチン接種の効果を判断する指標になるし、後者では禁煙の効果を判断する指標になる。
オッズ比との違いは何処にあるのであろうか、この例でいうとオッズ比は例えば暴露群での場合は病気になった人(事象)とならなかった人(非事象)の比率をいうのであるからa/bである。
このような例の場合には、オッズ比よりも相対危険度の方がわかりやすい。
⑧ 尤度比*3
尤度の原語であるlikelihoodは「ありそうなこと」、「見こみ」、「公算」という意味であるが、尤度の「尤」は「特別なこと」、「異なること」、「優れたこと」、「罪」、「過ち」という意味であり、原語の意味とは若干違っているように見えるが、「尤も」という意味は、「如何にも理屈に合っている」という意味だが、「そうは言うものの」という意味もあるので、「尤度」という訳は適切かどうかわからないけれど、「もっともらしさ」とか「見こみ」という意味合いで用いられたと解釈したい。
尤度比は、その尤度の比率のことであるが、その7(平成12年10月号)で書いた感度や特異度などの効果指標より新しい概念で、その検査のもっともらしさを表す指標となるといえる。
ここで少し復習をすると、感度(敏感度)は、疾病を実際に持つ患者がその検査で陽性となる確率を表しており、特異度はその反対に、疾病を持たない患者にその検査で陰性になる確率を表している。それに対して、陽性反応的中率は検査での陽性者が実際に疾病を有している確率を示している。
尤度比は、 感度/(1-特異度) で表され、その7に於ける図8では、
尤度比 = 分子 a/(a+c)分母 b/(b+d) となる。
すなわち、疾病を持っているものが正しくと陽性になる確率と疾病を持ってないものが間違って陽性になる確率の比で表され、分子に正しさ、分母に間違い度が来るために、この比率が高ければ高いほど検査が有効であることを示す数字となる。この場合は陽性になることの有効性を見るので陽性尤度比という。
その逆に検査の陰性の尤度比は、 (1-感度)/特異度 で表され、図8で
言えば 陰性尤度比 = 分子 c/(a+c)分母 d/(b+d) となる。
これは、疾病を持っているのに検査で陰性になった割合と疾病を持ってない者が正しく陰性の結果になった割合の比で、陽性尤度比と違って正しい結果が分母に、誤った結果が分子に来るために値が低ければ低いほど良い検査(その病気でないことと除外するために)ということになる。
ではその7の図9~図12を用いてTOS(胸郭出口症候群)の諸検査の尤度比を計算してみる。
Adson’s testは 陽性尤度比=54.8 陰性尤度比=0.74 となり、このテストの陽性反応的中度と陰性反応的中度は共に90%前後で陰性の場合も陽性の場合もその価値は同等ということであったが、尤度比で見ると、テスト陽性の価値は高く、陰性の価値は低いという結果になった。
Wright’s test は、陽性尤度比=1.64 陰性尤度比=0.45 となり、陽性反応的中度は13%も低く、やはり陽性の場合には当てにならないが、陰性反応的中度は96%と高いことも有り、陰性の場合には若干であるが有効性が有る検査といえるようである。
Morley’s test では+2と+3を陽性とした場合 陽性尤度比=11.1 陰性尤度比=0.39 となり、陽性反応的中度は66%、陰性反応的中度は94%であったが尤度比で見る限りにおいては有効性が比較的高いテストと言える。
3分間テストは、陽性尤度比=161.1 陰性尤度比=0.024 となり、陽性反応的中度94%、陰性反応的中度98%といずれも高く、尤度比も的中度も最も有効性の高いテストという結果となった。
陽性反応的中度や陰性反応的中度は、患者の立場や鍼灸師が出来ない検査結果を患者から聞いた鍼灸師の立場では、最も重要な指標であるが、尤度比は検査を評価する立場や検査を用いる立場では最も重要な指標ということが言えるだろう。
また、感度や特異度は陽性か陰性、すなわち有るか無いかのデジタルに二分割出来る検査項目に対して用いられるものだが、一般的な検査の多くは、例えばγ-GTPは40mU/ml以下が正常でそれ以上が異常というようなものである。この場合にこの40mU/mlというカットオフポイント(*4陽性と陰性の境目)で切って、それ以上を陽性、それ以下を陰性としてしまうと、例えば、γ-GTPが50mU/mlの場合と、100以上の場合では肝炎や肝癌などの疾病を示唆する材料としての価値が違ってくるわけであるが、そのような情報は失われてしまうことになる。
臨床的には、血清学的な血液データは、いわゆる標準値や正常値だけで判断することは少なく、他の所見や他の臓器の検査データ、及び患者の生活史などを総合して判断するわけであるが、そうは言ってもγ-GTPだけでみて50mU/mlと200mU/mlでは、診断上に大きな差異が生じるであろう。尤度比は、この点に一つの客観的な目安を与えてくれる重要な指標である。(カットオフポイントの項参照)
⑧ カットオフポイント
図8のMorley’s test で、+2以上を陽性というカットオフポイントを変えて見た場合の尤度比は、+1以上を陽性として場合には、陽性尤度比が3.0、陰性尤度比は0.21で陰性は使えそうであるが、陽性は使えそうにない。また、+3以上を陽性とした場合には、陽性尤度比は15.4、陰性尤度比は0.76でこの場合には陽性は使えそうであるが陰性は使えそうにないという結論になる。このようにカットオフポイントの位置によって、尤度比は変化し、確定診断に適切な診断と、除外診断に適切な診断に分けることが出来る。(表18)
しかし、簡単に言えば、+1は鎖骨上窩部の圧痛のみがあるものであり、+3は指先まで放散痛が有るものであるから、当然より病的(病気がありそう)であるし、+1も無い者は病気でない可能性が高いのは当然である。ただ、尤度比はこの当然というややもすると思いこみになりがちなものに、数値で表してその妥当性の基準を示してくれるところに大きな価値が有る。
そして、尤度比及び陽性反応的中率などでMorley’s test を判定すると、肩以遠まで痛みが放散する場合には、病気有りと判断し、圧痛がない場合には病気無しと判断する診断法が最も誤りが少ない診断法であると結論できる。
γ-GTPのようにデータが連続量*5の場合には、このカットオフポイントをどこに持っていくかで尤度比が違ってきて、この分析が出来ていればより確率の高い診断が行えるようになるのであるが、実際には、日本人またはその病院の外来患者、または健康診断での平均値に上下に標準偏差の2倍程度の幅の範囲を設け、その中に入っていれば正常、それに外れれば異常というようにしている。分かりやすくいえばいわゆる偏差値の30~70の範囲は正常で、それ以外は異常ということである。この異常は通常上の異常が2.2%程度で、下の異常も同じ2.2%であるから、95.6%の人は全て正常になる。これは標準偏差(σ)の2倍の範囲で設定したので2σの範囲といわれる。場合によっては3σ(正常は99.7%)迄拡大することもある。
この方法は分かりやすいが、あくまでも平均的な人は健康であるという前提が必要である。例えば肥満や痩せを考えると、この飽食な時代日本人全体が肥満気味であるのでこの前提は簡単に崩れる。あくまでも実際の病気の有無と、数値との関連から考えられるべきだと思うが、例えば血圧のように部分的には解明されている(ガイドラインが出来た)ようであるが、まだまだ不十分である。
⑨ SnNoutとSpPin
SnNoutのSnは、Sensitive(感度)を表し、感度が高い検査では陰性(N:Negative)が出たらout(rule out:除外する)するということを意味している。一般的に感度が高い検査(病気がある場合の陽性率が高い)では、陽性が出たら当該の病気である確率が高いと思いがちであるが、感度が高い検査では陽性よりも陰性に価値があり、陰性が出たらその検査が示唆する病気はないと判断しても間違いが少ないということである。
SpPinのSpは、Spcificity(特異度)を表し、特異度が高い検査では、陽性(P:Positive)が出たら、in(rule in:診断する)ということを意味している。これはSnNoutと反対に、特異度が高い検査(病気がない場合に陰性となる率が高い)では、陽性が出たら積極的に当該の病気と診断しても良いということを意味している。
感度は、病気の場合に陽性と成る率が高いことを意味しているので、その検査の価値が高いと思われるが、検査の価値はともかく診断上は陰性となった場合の方が尤度比は高いのである。実際に特異度が99.5%と高いAdson’s testでは、陽性尤度比=54.8 陰性尤度比=0.74 で陰性になったときの尤度比は除外するには値が高すぎるが、反対に陽性の尤度比は診断を確定するに値するほど充分高いのである。また、比較的感度が高い(75.4%)Wright’s test は、陽性尤度比=1.64 陰性尤度比=0.45 で陽性尤度比は全く問題にならないくらい低いが、陰性尤度比は特異度が54%と低いのに関わらず、除外するに参考になる数値では有る。
このことは、あらゆる検査に云えることで、通常は全く逆に考えてしまうが、良く考えれば当然のことである。この尤度比という概念を導入することによって、このことに気がついたし、確かめられたsackett 教授は述べている。
日本語で強調すると「感度が高い検査で陰性が出たら、自信を持ってその病気でないと診断し、特異度が高い検査で陽性が出たら、堂々とその病気であると診断せよ」ということである。ただし、もちろん百%ではないが。
英語だと覚えやすく出来ている言葉で、Sn(Sensitive)のnならN(Negative)で陰性を(陰性だから当然)除外し、Sp(Spcificity)のpならP(Positive)で陽性を(陽性だから当然)採択する、という具合である。
⑨ 検査前確率*6と検査後確率*7
有る疾患を患者が心配になって病院を訪れたとしよう。その疾患に罹っているかどうかはわからないが、その病気になっている確率は当然誰でも有るだろう。一般的には、国民の健康白書などに記載されている、年齢別の有病率がその一つの数値を与えてくれる。例えば、日本国民の五十歳代男性で肝硬変の有病率は、集計の問題で1・2年のタイムラグはあるにしても、大きな変動はないであろうから、既にわかっているといって良いであろう。そして、日本の五十歳代男性のすべてに血液検査をする場合に、その病気である確率(検査前確率)は既知といって良い。そして検査をして、例えばγ-GTPが90mU/mlの人は検査結果から、検査をする前の肝硬変である確率から、より高い確率に変わると考えられる。これが検査後確率である。
この検査後確率は検査前確率と尤度比によって求めることが出来る。
この場合計算式が複雑になるので、検査後オッズを求めてから変換するの普通である。
検査後オッズ=検査後確率/(1-検査後確率)
=検査前オッズ×尤度比
={検査前確率/(1-検査前確率)}×尤度比
={検査前確率/(1-検査前確率)}×{感度/(1-特異度)}
と計算され、検査後確率は 検査後確率=検査後オッズ/(1+検査後オッズ) で求められる。そしてこの検査後確率は陽性反応的中度と同じになる。陽性反応的中度は、陽性になった場合に、疾患がある確率をいうわけであるから、まさに検査後確率になる。
計算は面倒くさいが、四則演算だけなので簡単である。図8でいうと検査前確率は、全体のN(=a+b+c+d)を分子にして疾病があるa+cを分子にすればよいので 検査前確率=(a+c)/N と書ける。
1-検査前確率は {(a+b+c+d)-(a+c)}/(a+b+c+d)
だから(b+d)/Nとなる。
よって、検査前確率/(1-検査前確率)=(a+c)/(b+d)である。
尤度比は感度=a/(a+c) 1-特異度=b/(b+d) で
尤度比=a(b+d)/b(a+c) となる。 そして、検査後オッズは
{検査前確率/(1-検査前確率)}×尤度比=a/b となって
検査後確率は (a/b)/(a+b)/b=a/(a+b)となり、これはまさに陽性反応的中率である。
<SLRで30度以下で陽性ならば椎間板ヘルニアか?>
椎間板ヘルニアがある場合にSLRが30度以下で陽性になることが多い(感度が高い)ということが良くいわれるが、SnNoutの原則で、30度以下で陽性でなければ「椎間板ヘルニアでない」といって良いというわけではない。我々鍼灸師が行う場合には、確定診断が後なので、陽性所見があって病院で調べたら椎間板ヘルニアがあることが多いということであるから、鍼灸の学会等で報告されているのは、感度が高いということでなく陽性反応的中度すなわち検査後確率が高いということであるから、このSLRの件は陽性ならば、ヘルニアである確率が高いということをいっている。しかし、残念ながら陰性であった場合のヘルニアの確率や陽性であった場合のヘルニアでなかった確率などが分からないのでEBM的には言えない。
<大学病院でのデータを使ったTOSの検査結果は鍼灸院でも使えるか>
胸郭出口症候群についてのEBM的な分析により、Adson’s testは陽性所見で意義があり、Morley’s test は+2以上の陽性と圧痛もない-の所見に意義があり、3分間テストは陽性・陰性ともに意義があるという結果は、そのまま鍼灸院でも使えることなのであろうか。
検査前確率は、キーワードのところで説明してあるように、病院と鍼灸院では違うし、症状を持っている人と持ってない人では違う。TOSで引用したデータは大学病院のデータであるので、この病院における検査前確率と鍼灸院での検査前確率は当然違っていると考えるのが普通である。外来患者は大学病院であろうと鍼灸院であろうと、症状があるから受診するのであるから、この点では両者に差はない。しかし、一般的には症状が重い人は大学病院の方を選択するであろうことは常識的な推測である。よって、検査前確率(有病率)は違うと考えるのが自然である。そして、検査後確率は、検査前確率と尤度比によって左右されるわけであるから、検査前確率が違えば検査後確率=陽性反応的中度が違ってくると考えるのは自然である。
では実際にそうなるであろうか。表19は、3分間テストの有病率(検査前確率)を約半分にした表である(正常群はそのままの数値を使い、患者群を約半分にした:鍼灸院の来院患者は大学病院の外来患者よりも実際に病気である人の割合が半分であると仮定して)。この表を元に各種指標を計算してみると、感度79.3%(78.3:福岡大学のデータの感度、以下同じ)、特異度99.5%(99.5)、陽性反応的中度88%(94)、陰性反応的中度99%(97.9)、尤度比163(161)となり、感度、特異度、尤度比は変わらないが陽性反応的中度と陰性反応的中度は若干変わる。理論的にも、有病率は感度と特異度に関わらないので、尤度比も変わりないが、陽性反応的中度と陰性反応的中度は変わってくる。試しに有病率を1/4にすると、陽性反応的中度は80%迄減じ、陰性反応的中度は99.5%迄になる。
私には非常に奇異な感じがする結果であった。検査で陽性な場合に、その陽性者が実際に疾患を有しているか否かの確率は、その施設の患者層によって左右されるということは、私などの頭の固い人間にはなかなか理解が難しい。しかし、例えば肝臓病専門の病院で、肝臓が実際に悪いと感じている人が多く来院している場合に肝機能検査で異常が出れば、肝臓が特に悪いと思ってない、例えば一般の定期検診などでの陽性者よりも、肝臓病専門の陽性者の方が実際に肝臓病である確率が高いというのも自然なことようにも思える。
EBMは、このように人間の「思いこみ」や「勘違い」を正してくれる道具という解釈もできそうである。 つづく
<今日のキーワード>
*1 オッズ比(odds ratio):オッズは事象に対する非事象の比率のことで、オッズ比は実験群がある要因に暴露するオッズを対照群のオッズで割ったオッズの比のこと。例えば、もし疾患が起こるという事象率(確率)が0.2(20%)なら、非事象率は0.8でオッズは8:2(2/8=1/4)となる。これは事象率(確率)の逆数ではないことに注意。事象率の逆数ならば、5:1 となる。すなわち事象率(起きる確率)がpならば、オッズ比はp/(1‐p)で表される。または総数がnでその内a回起きるのならばオッズ比はa/(n‐a)で表され、事象率はa/nである。
oddsはoddの複数形で、oddは奇数や半端なとか奇妙なという意味である。
*2 相対危険度(relative risk:RR):試験群の事象率(危険率)を非対照群の事象率(危険率)で割ったものをいう。
*3 尤度比(likelihood ratio):有病者がその検査結果(例えば陽性)となる確率と、非有病者が同じ検査結果(つまり誤り)になる確率の比率で、尤度比=感度/(1-特異度)、または(1-感度)/特異度 と定義される。一般的には、尤度比は10以上なら確定診断に、0.1以下ならば除外診断に使えるが、5以下及び0.5以上はあまり有効とは言えないがあくまでも目安である。
また、陽性か陰性の二つしか結果がない場合でもカットオフポイントを変えれば当然尤度比は変化する。
*4 カットオフポイント(Cut off point):図17のように検査値にバラツキがある場合に、ある値で切って、それ以上(またはそれ以下)を異常と判定し、それ以下(またはそれ以上)を正常と判定する値のことをカットオフポイント(カットオフ値)という。図17において、この値を右に移動すると健常者を異常と判定することは少なくなるが、逆に異常者(疾病がある者)を正常とする確率が高まる。また、その逆にカットオフポイントを左に移動すると異常者を正常と判定する確率は下がるが、逆に健常者を異常と判定する確率が高まる。
*5 連続量:データが陰性か陽性か、または鍼灸師、医師などの職業のような離散量(カテゴリー)でなく、1,2,3,‥‥10,‥‥100,‥‥200,‥‥のように繋がっている量のことで、厳密には小数点以下も当然あって0.0112とか19.569というような数値もあるものをいうが、実際には有効数字の問題があり細かくしても意味がないので整数だけで扱うこともしばしばである。整数しかない数字の場合には連続量とはいえないが、1と2との距離(違い)とある数値nとn+1の差が同じ場合(このように間隔が同じ量を間隔尺度という)には通常連続量として近似している。
*6 検査前確率(事前確率:prior probability):検査を実施する前に疾病があると判断される可能性を示す確率のことで、有病率が集団に対して用いられるのに対し、検査前確率は個人に対して用いられる。しかし、大病院に来院する患者と町の一般開業医に来院する患者では、患者の病態像が違うために当然この確率は変わってくるだろうし、米国での検査前確率と日本でも違うし、同じ病院でも入院患者と外来患者でも違うであろう。もちろん、季節変動や地域差・環境差も当然あると考えられ、すべて有病率だけで判断できるわけではない。
*7 検査後確率(事後確率:posterior probability):検査を実施した後に検査の結果と疾病の存在が一致している確率のことで、陽性反応的中率と一致する。陽性反応的中率や陰性反応的中率は集団に用いられるのに対し、検査後確率は個人に対して用いられる。この値も検査前確率と尤度比に影響されるために、これらの数値が変われば、検査後確率も変わる。
<引用・参考文献>
1)北澤京子「癌集団検診の有効性を問い直す」日経メディカル 1997年8月号 p71-74
コメント